avalable LSST talk

Forecasting the power of Higher Order Weak Lensing Statistics with automatically differentiable simulations

Denise Lanzieri










slides at github.com/dlanzieri/talks/LSST_talk

the $\Lambda$CDM view of the Universe















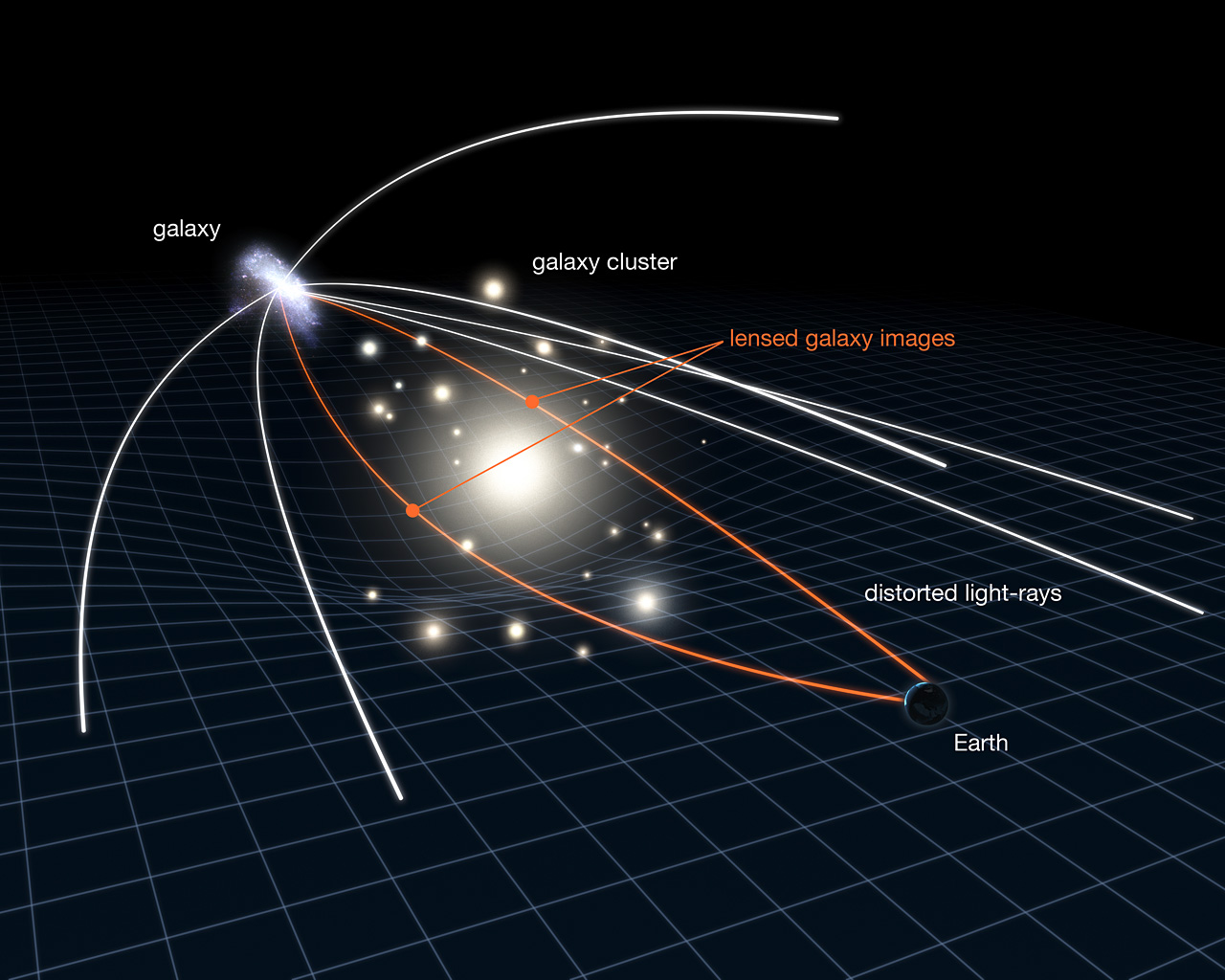
Weak Gravitational lensing

2 Point Statistics: A Suboptimal Measure

How do we make the most of the available data?

HSC cosmic shear power spectrum
HSC Y1 constraints on $(S_8, \Omega_m)$
(Hikage,..., Lanusse, et al. 2018)
  • Standard Weak lensing analysis:

    • Shear $\gamma$

    • Data reduction

    • Power spectrum
    Main limitation: The lensing convergence field is inherently and significantly non-Gaussian
    The two-point statistics do not fully capture the non-Gaussian information encoded in the peaks of the matter distribution

    $\Longrightarrow$ We are dismissing most of the information!

    How to maximize the information gain?

    Cosmological constraints from the combination of different summary statistics
    (Ajani, et al. 2020)
    • Approaches based on measuring high-order correlations to access the non-Gaussian information
      e.g. the Peaks count

    • Investigate the constraining power of various map-based higher order weak lensing statistics

    • How can we do that in a fast and accurate way?
      $\Longrightarrow$ Fisher Information

    Fisher Matrix

    \[\begin{equation} F_{\alpha, \beta} =\sum_{i,j} \frac{d\mu_i}{d\theta_{\alpha}} C_{i,j}^{-1} \frac{d\mu_j}{d\theta_{\beta}} \end{equation} \]
    • Use Fisher matrix to estimate the information content extracted with a given statistic

    • Derivative of summary statistics respect to the cosmological parameters.
      e.g. the $\Omega_c$, $\sigma_8$

    • Estimate derivative with final differences


    Numerical Differentiation

    \[\begin{equation} \left.\frac{df(x)}{dx}\right|_{x_1} \approx \frac{f(x_1+h)-f(x_1)}{h} \end{equation} \]
      Flaws :
    • It’s numerically very unstable

    • It’s very expensive in term of simulation time

    • Computes an approximation

    Different approach :

    Automatic Differentiation

    Automatic Differentiation and Gradients in TensorFlow



    • TensorFlow compute automatically derivatives of arbitrary order by applying the chain rule   repeatedly to elementary arithmetic operations

    • To differentiate automatically, TensorFlow remember what operations happen in what order during the forward pass and traverses this list of operations in reverse order to compute gradients.



      Advantages :
    • Derivative as functions

    • No numerical approximation

    • High speed

     Chain rule   :

    \[\begin{equation} \frac{dw}{du}=\frac{dw}{dv}\frac{dv}{du} \end{equation} \]

    Cosmological N-Body Simulations


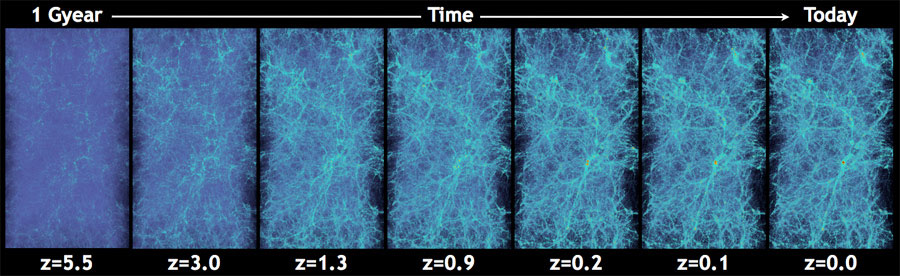
    How do we simulate the Universe in a fast and differentiable way?

    The Particle-Mesh scheme for N-body simulations

    The idea: approximate gravitational forces by estimating densities on a grid.
    • The numerical scheme:

      • Estimate the density of particles on a mesh
        $\Longrightarrow$ compute gravitational forces by FFT

      • Interpolate forces at particle positions

      • Update particle velocity and positions, and iterate

    • Fast and simple, at the cost of approximating short range interactions.
    $\Longrightarrow$ Only a series of FFTs and interpolations.

    Introducing FlowPM: Particle-Mesh Simulations in TensorFlow

    
											import tensorflow as tf
											import flowpm
											# Defines integration steps
											stages = np.linspace(0.1, 1.0, 10, endpoint=True)

											initial_conds = flowpm.linear_field(32,        # size of the cube
											100,       # Physical size
											ipklin,    # Initial powerspectrum
											batch_size=16)

											# Sample particles and displace them by LPT
											state = flowpm.lpt_init(initial_conds, a0=0.1)

											# Evolve particles down to z=0
											final_state = flowpm.nbody(state, stages, 32)

											# Retrieve final density field
											final_field = flowpm.cic_paint(tf.zeros_like(initial_conditions),
											final_state[0])

											with tf.Session() as sess:
											sim = sess.run(final_field)
    • Seamless interfacing with deep learning components

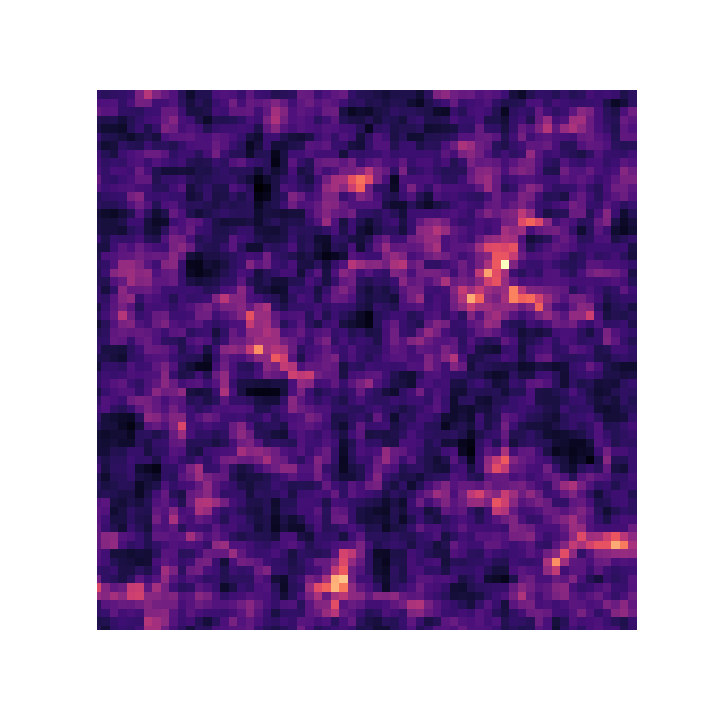
    Mocking the weak lensing universe:

    • We can map the distribution of all matter over cosmic time.

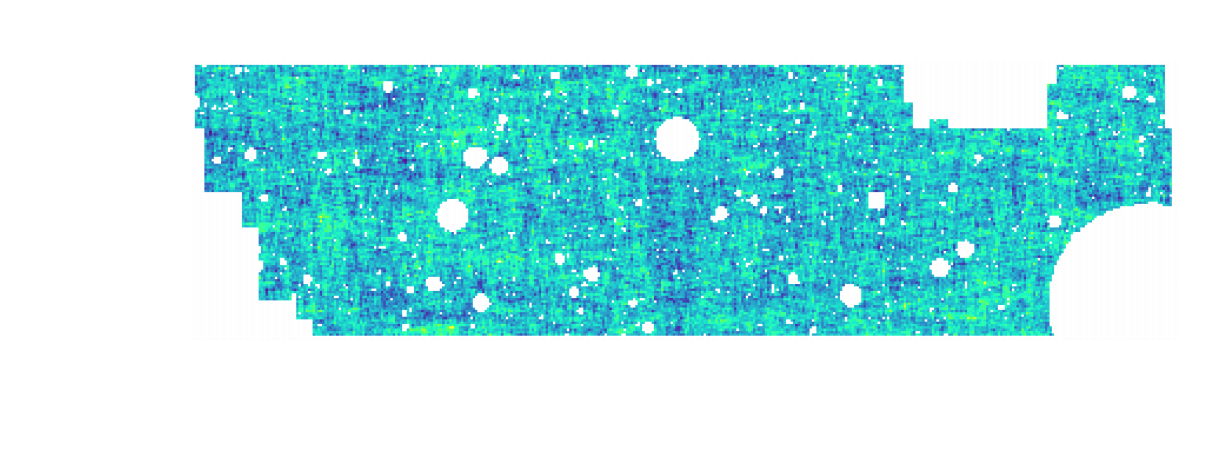
    • Convergence maps
      $\Longrightarrow$ weighted projection of the 3D cosmological mass density along the line-of-sight.

    • Access the signal in the convergence maps using a given statistic, e.g. Convergence power spectrum
    Convergence map at z=1.0, based on a 3D simulation of side length 256 Mpc/h and $256^3$ particles. (Böhm, et al. 2020)

    Mocking the weak lensing universe: The Born Approximation



    • Numerical simulation of WL features rely on ray-tracing through the output of N-body simulations​

    • Knowledge of the Gravitational potential and accurate solvers for light ray trajectories is computationally expensive

    • Born approximation , only requiring knowledge of the density field, can be implemented more efficiently and at a lower computational cost


    \[\begin{equation} \kappa_{born}(\boldsymbol{\theta},\chi_s)= \frac{3H_0^2 \Omega_m}{2c^2} \int_0^{\chi_s} d\chi \frac{\chi}{a(\chi)} W(\chi,\chi_s) \delta(\chi \boldsymbol{\theta},\chi). \end{equation} \]

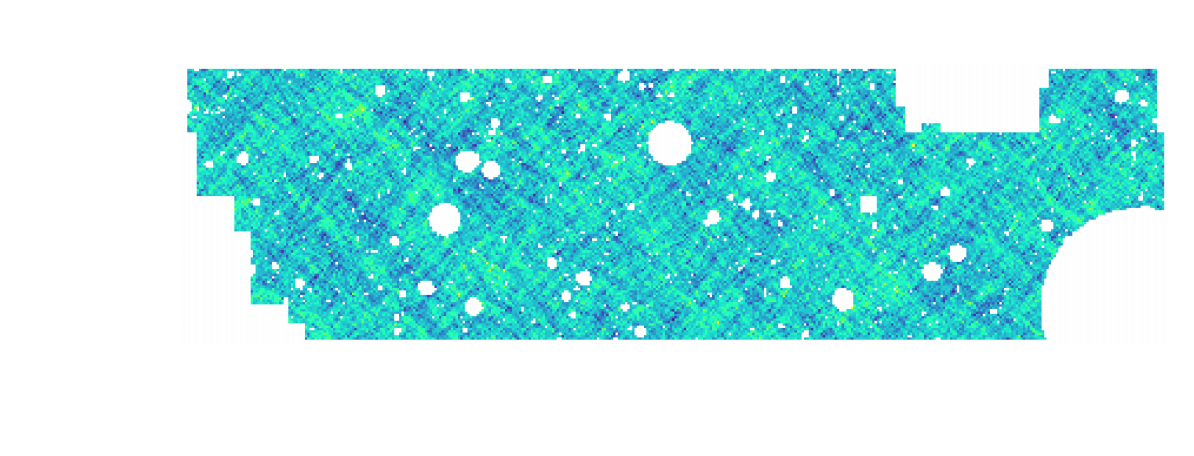
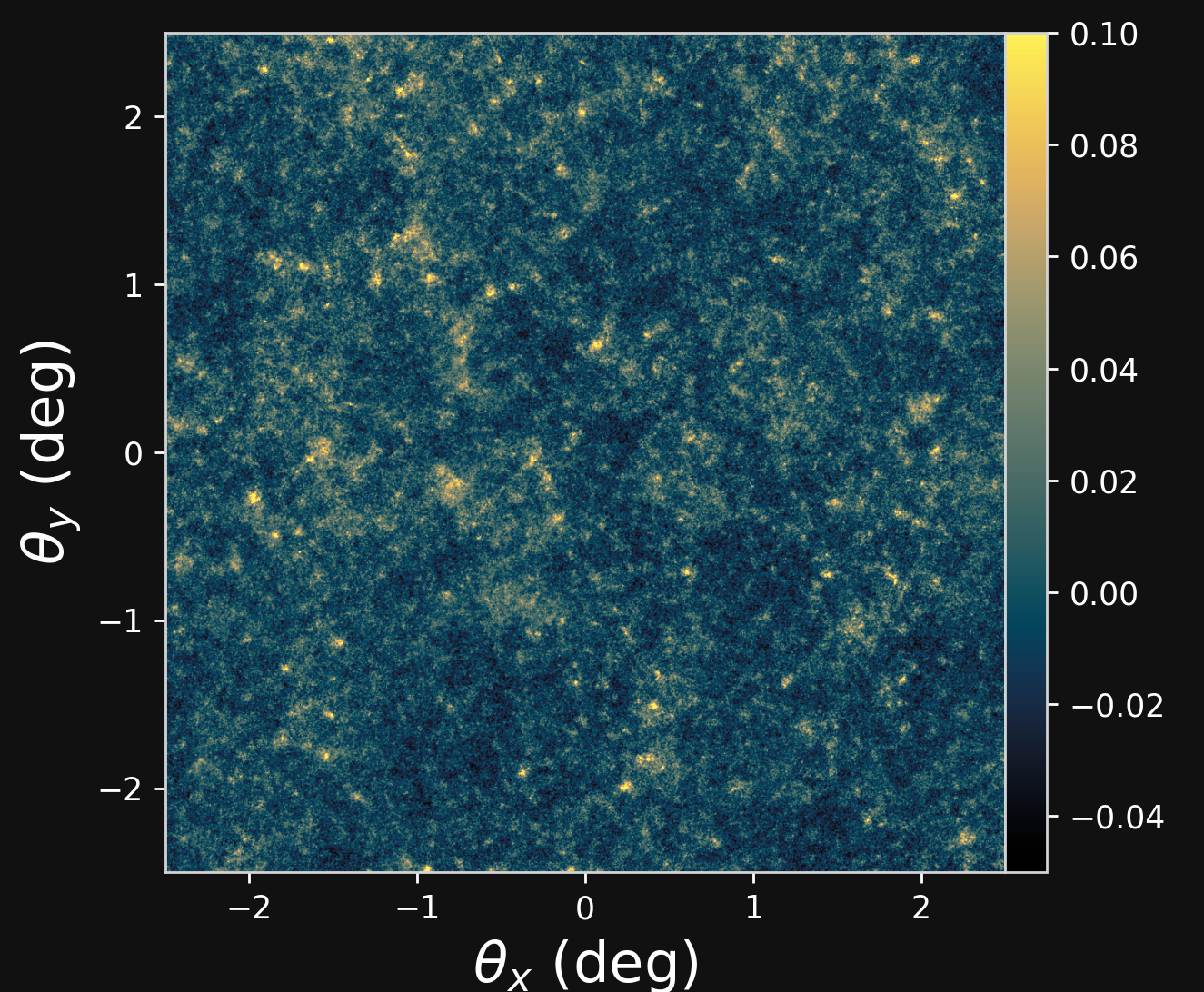
    Raytracing Validation

    We simulate lensing lightcones implementing gravitational lensing ray-tracing in FlowPM framework

    Proof of Concept

    • Convergence map at z=1.0, based on a 3D simulation of $64^3$ particles for side. The 2D lensing map has an angular extent of $5^{\circ}.$

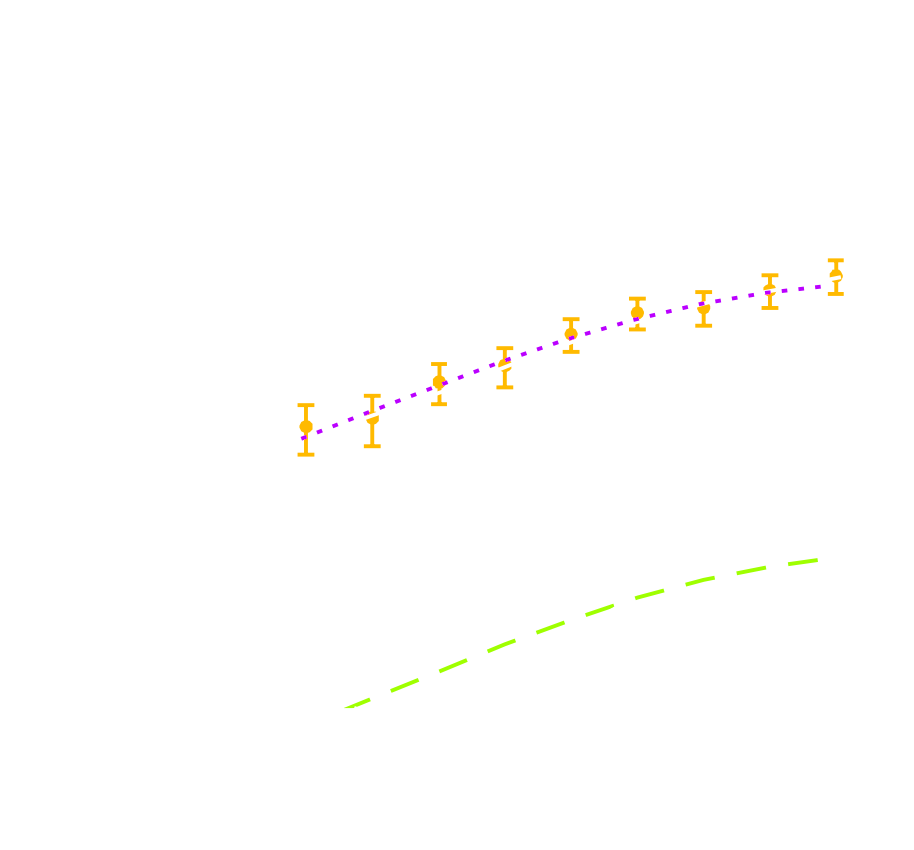
    • Angular Power Spectrum $C_\ell$

    • The Jacobian: \[\begin{equation} \frac{dC_l}{d\Omega_c}, \frac{dC_l}{d\sigma_8} \end{equation} \] \[\begin{equation} F_{\alpha, \beta} =\sum_{i,j} \frac{d\mu_i}{d\theta_{\alpha}} C_{i,j}^{-1} \frac{d\mu_j}{d\theta_{\beta}} \end{equation} \]
    • Constraints on cosmological parameter $\Omega_c$ and $\sigma_8$:

    Status and Next steps



    • Distributed version of FlowPM on several GPUs to generate large-scale mass-maps

    • Peak counts statistic implement in TensorFlow framework
      • Weak lensing peaks trace regions where the value of the convergence field is high $\Longrightarrow$ they are associated to massive Structures.
      • We compute peaks as local maxima of the signal-to-noise field

    • Compute summary statistic higher than second order to extract non-Gaussian cosmological information and infer cosmological parameters

    Conclusion

    Conclusion

    What can be gained by simulating the Universe in a fast and differentiable way?

    • Differentiable physical models for fast inference
      • Forecasts on differentiable higher-order statistics, including peak counts, etc.


    • Investigate the constraining power of various map-based higher order weak lensing statistics





    Conclusion

    Everyone is most welcome to join! How to get in touch:



    Thank you !